神戸大学大学院システム情報学研究科の谷口隆晴准教授、博士後期課程の学生の陳鈺涵さんと、大阪大学大学院基礎工学研究科の松原崇准教授らの研究グループは、一般の観測データから、データに隠された運動方程式を抽出することで、物理学に忠実なモデルを作成する人工知能技術の開発に成功しました。
今後、この技術により、これまで力学の理論で説明できないと考えられていた現象に対して、隠された運動方程式を発見できるかもしれず、例えば、生態系の持続可能性の検討に物理学の知見や物理シミュレーションが応用できる可能性があります。
この研究成果は、2021年12月6日から開催の、人工知能技術に関するトップ会議「Thirty-fifth Conference on Neural Information Processing Systems (NeurIPS2021)」で、採択率が約3%である Spotlight 枠で採択され、発表されました。
ポイント
- 人工知能を用いて物理現象のモデル化(数式化)が可能となれば、シミュレーションの高精度化・高速化につながる。
- 今までの人工知能を用いた方法では、運動方程式に従うようにデータを変形して与える必要があり、運動方程式が未知であるような実際の観測データに適用することが困難であった。
- 本研究では、幾何学を応用することで、どのような形式で観測データが与えられても、そこに隠された運動方程式を見つけ、それに従ったモデル化が出来る人工知能技術を開発した。
- 生態系の変化など、従来、ニュートン力学の対象ではないと思われていた現象に対して、隠された物理法則を発見できる可能性がある。
- そのような現象に対して、物理学の理論を応用した考察やシミュレーションが行えるようになり、未知の性質が解明される可能性がある。
研究の背景
通常、物理現象の予測はスーパーコンピュータなどのシミュレーションによって行われます。シミュレーションでは、物理学などに基づいて作成された数理モデルが使われていますが、信頼性の高いモデルがなければシミュレーション結果の信頼性も失われるため、現象の観測データから信頼性の高いモデルを作成する方法が重要となります。また、近年、物理学の適用範囲が予想外に広く、生態系の変化を表すモデルの一部などにもニュートン力学の理論が適用できる可能性が指摘されています。しかし、多くの場合、具体的な運動方程式などはいまだ明らかになっていません。
研究の内容
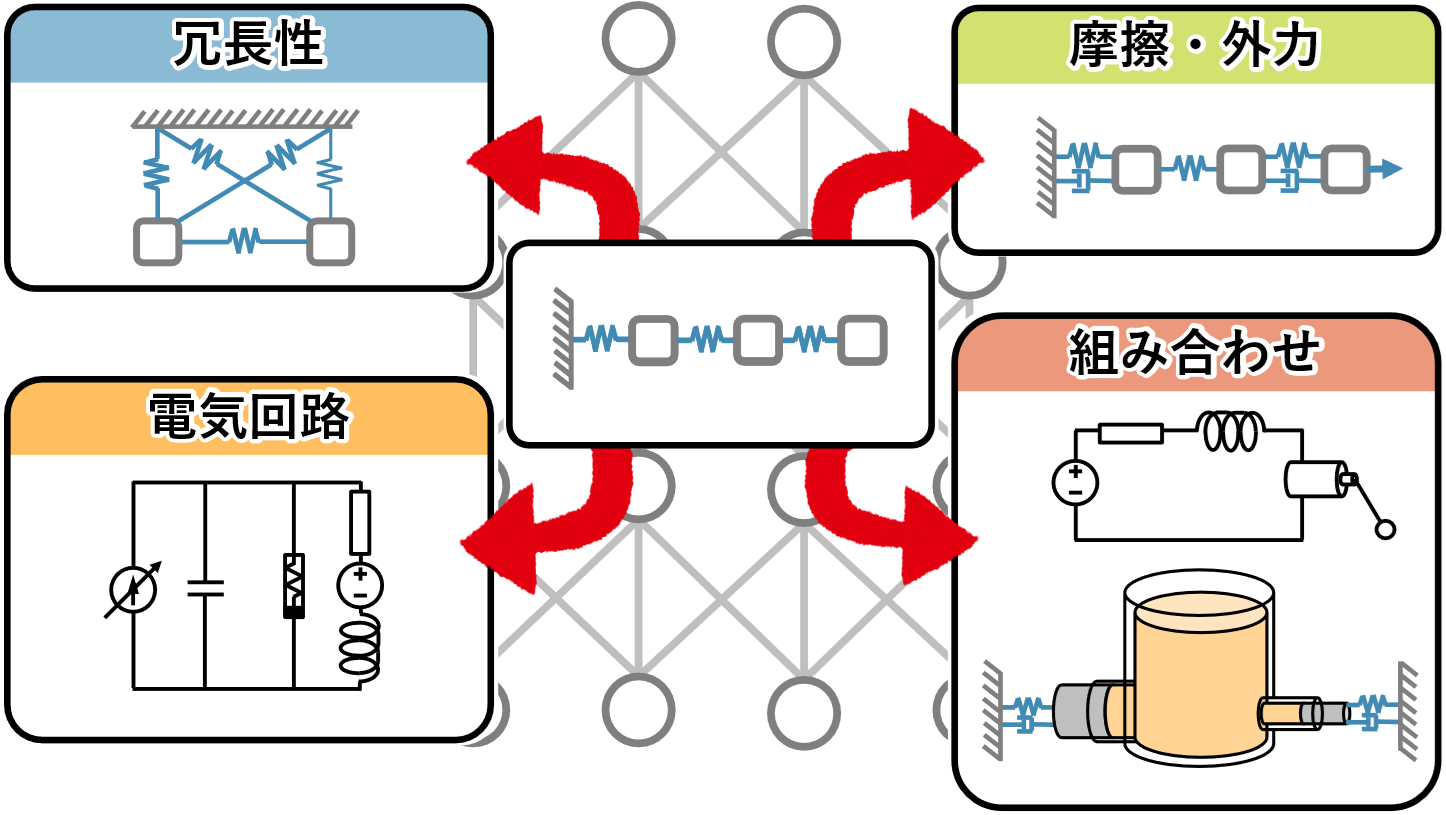
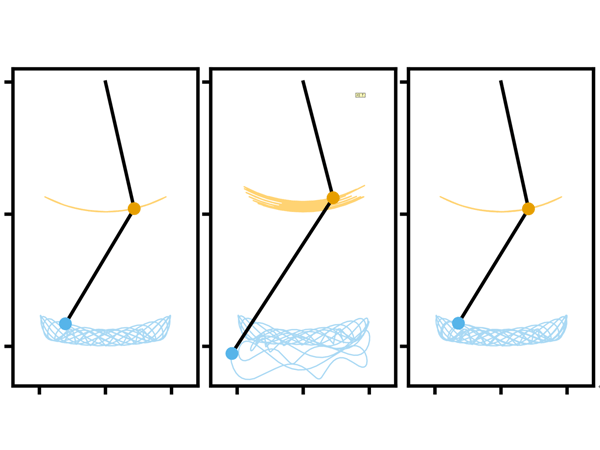
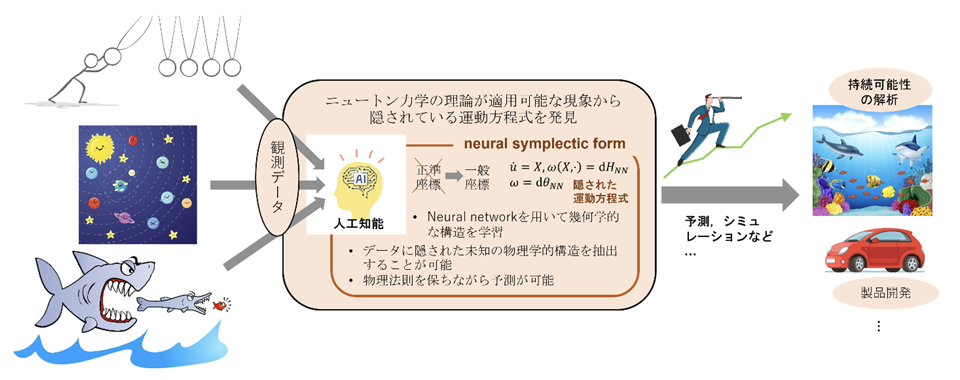
本研究では、ニュートン力学の理論が適用可能な現象の観測データから、新たな運動方程式を発見する方法を開発しました。これまでの研究でもデータから運動方程式を発見する研究は進められていましたが、既存の方法では特別な形の運動方程式が仮定されており、それに合わせて適切な形でデータを用意する必要がありました。しかし、実際には、どのような形でデータを用意すれば良いかが不明な場合が多く、現実的なデータに適用することは困難でした。
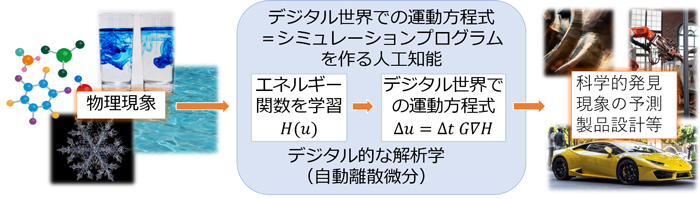
これに対して、本研究では、観測データを適切に変形することを幾何学における座標変換と考え、物理学のもつ座標変換不変性という幾何学的な考え方を応用することでこの問題を解決しました。そのためには、現象の背後にある未知の幾何学的な性質を解明する必要がありますが、本研究では、データからこの幾何学的性質を発見する人工知能技術を開発することに成功しました。これによって、データに潜む運動法則を抽出することが可能となり、それを利用することで物理学に忠実なモデルとシミュレーションが出来るようになります。
今後の展開
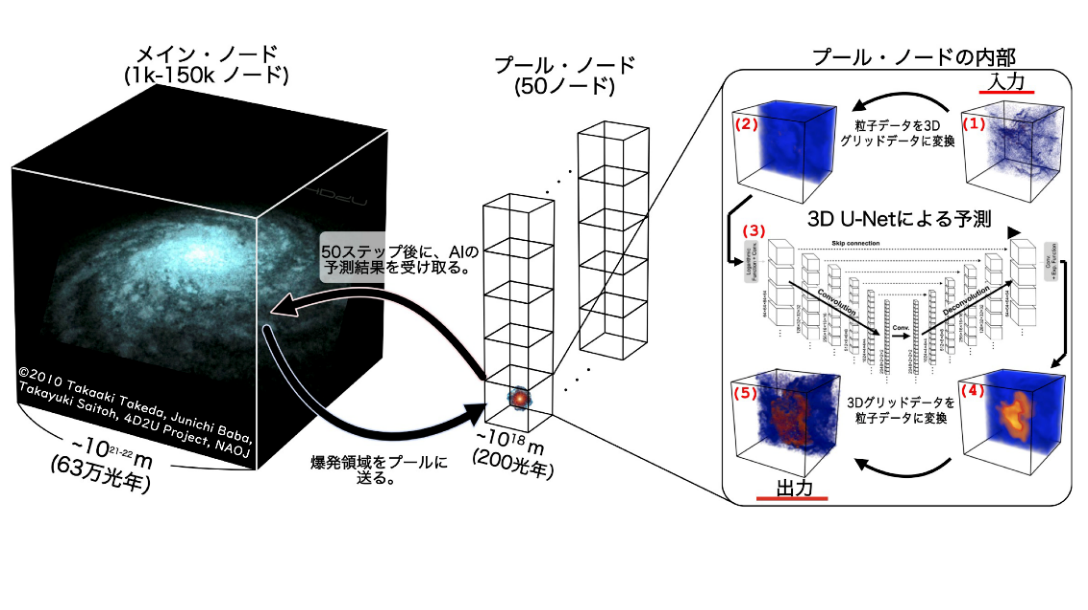
気象予報、創薬、建造物の解析、車体設計のための空力計算など、さまざまな分野で物理シミュレーションは行われていますが、通常、その際には膨大な計算を必要とします。ですが、この手法によって対象となる現象のデータを学習し、未知の小さなモデルを構築することが出来れば、物理法則を守りながら計算を簡略化・高速化することができ、これらの分野の発展に寄与する可能性があります。
また、データには、一見、物理学に無関係に見えるようなものを利用することもできるため、そのような場合に運動方程式が抽出出来れば、これまで物理学で説明できないと考えられていた現象に対しても、物理学の知見を生かした考察やシミュレーションが出来るようになる可能性があります。例えば、生物の個体数のデータから、個体数変動を表す隠された運動方程式を見つけ、生態系の持続可能性の検討に、エネルギー保存則などの物理学の理論が応用できる可能性があります。
謝辞
本研究は、以下の支援を受けて行われました。
- 科学技術振興機構(JST)戦略的創造研究推進事業 チーム型研究(CREST)
研究領域:「数学・数理科学と情報科学の連携・融合による情報活用基盤の創出と社会課題解決に向けた展開」(研究総括:上田 修功)
研究課題名:「幾何学的離散力学を核とする構造保存的システムモデリング・シミュレーション基盤」(JPMJCR1914)(研究代表者:谷口 隆晴)
論文情報
- タイトル
- “Neural Symplectic Form: Learning Hamiltonian Equations on General Coordinate Systems”
- 著者
- 陳鈺涵1、松原崇2、谷口隆晴1
1 神戸大学大学院システム情報学研究科
2 大阪大学大学院基礎工学研究科 - 掲載誌
- Advances in Neural Information Processing Systems 34 (NeurIPS 2021)