光は、あらゆる生物観測において重要な役割を果たしています。光を細胞や組織断片などに照らすことで、ながらく生物イメージングを行なってきましたが、いまだに、光伝搬の鍵となる細胞内の不均一性における光学効果については明らかではありませんでした。今回、自然科学研究機構 生命創成探究センター (ExCELLS) の渡部匡己特任准教授は、神戸大学 次世代光散乱イメージング科学研究センターの的場修教授らと共同で、光が細胞内の屈折率乱流を伝搬した時の物理プロセスをモデル化するだけでなく、蛍光イメージングから細胞内の屈折率ゆらぎ・フラクタル次元・散乱係数などの光学的特性を計測することに成功しました。これらの研究成果は、今後、細胞内の不均一な空間分布によって引き起こされる光散乱やゆらぎなどの光学効果を細胞モデルに同時に組み込むことで、生物顕微鏡イメージングのより現実的なシミュレーションの実装に繋がることが期待できます。
本研究成果は、国際科学雑誌 「Physical Review Research」(2023年5月30日付) に掲載されました。
ポイント
- 光が細胞内の屈折率乱流を介した時の光学プロセスをモデル化
- 蛍光イメージングから細胞内の光学フラクタル特性を計測
- 生物画像シミュレーションの拡張実装に期待
背景
細胞は生命の基本的な構造・機能の単位を担っており、生体分子(タンパク質や核酸など)と細胞内小器官(小胞体、ゴルジ体、ミトコンドリアなど)を含む、膜で閉じられた細胞質から構成されています。これらの複雑な内部構造は、光学イメージングシステムや電子顕微鏡を用いて可視化することができます。しかし、光学イメージングでは、可視光の波長が360~760 nmで、電子の波長より5桁も長いため、電子顕微鏡で観察できるような小さな細胞内物体の構造を捉えることはできません。
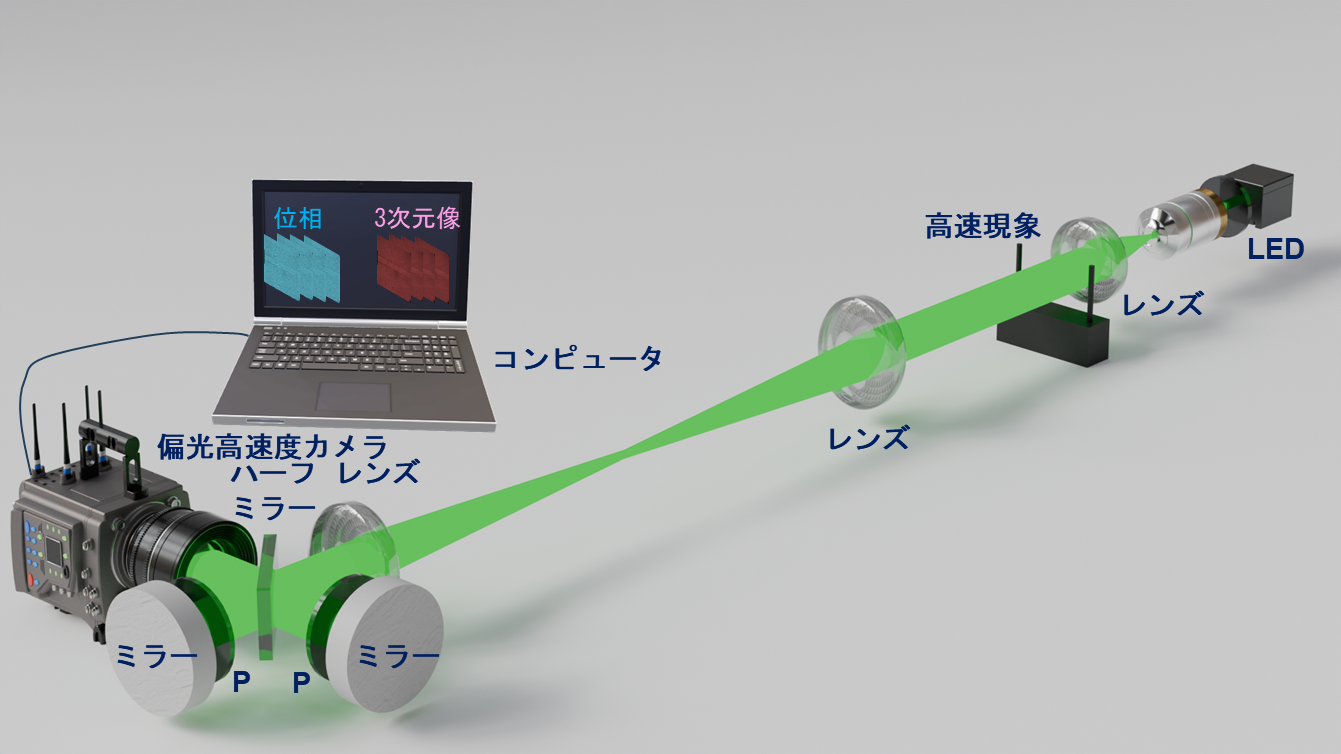
顕微鏡観測における波動関数の複素振幅は、「強度」と「位相」の2つの物理量から構成されています。これら物理量の相互変換は、特に、強度輸送方程式(Transport of Intensity Equation: TIE)と呼ばれる偏微分方程式として定式化されており、医療画像(例えば、X線CTや光学CT)などの解析によく利用されています。しかし、この方程式は、一般的に、中間場(すなわち光子と電子)を記述する波動関数の強度分布が任意の位相空間を通って伝搬することを仮定しているため、細胞内部の複雑な屈折率乱流を介した時の強度変化について表現することはできていません。
本研究の内容
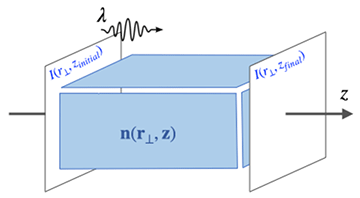
任意の波長λを持つ平面波の強度分布I(r⊥,zinitial)が、細胞内の屈折率分布n(r⊥,z)を伝搬して、最後に強度分布I(r⊥,zfinal)が出力されることを示す。
(1) TIEの再公式化
TIEは、ある波長の中間場における強度と位相の数学的関係性を表現しており、特に、光学顕微鏡法と電子顕微鏡法の間に横たわる大きな分解能のギャップを埋める上で重要な役割を果たしています。本研究では、任意の位相空間を仮定するのではなく、細胞内の屈折率乱流を表す光学フラクタルモデルを用いて、TIEの再公式化を行いました (図1)。
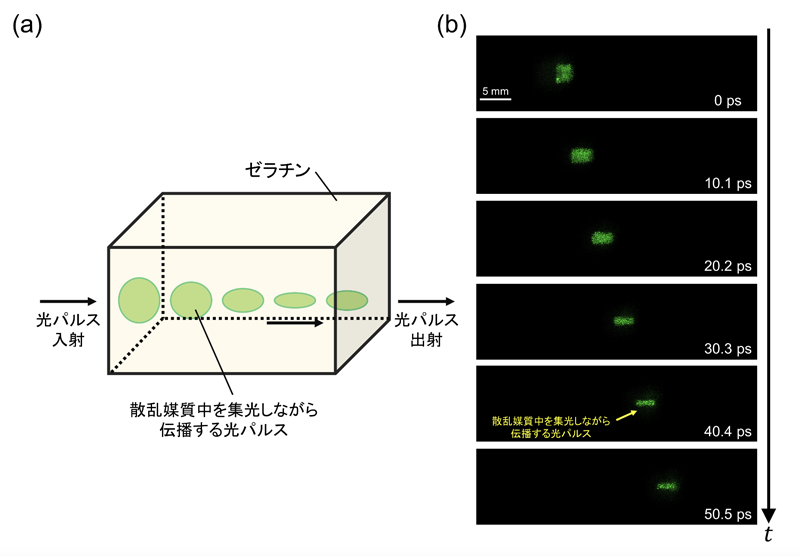
(2) 光が細胞内部を伝搬する物理プロセスのシミュレーション
広範囲の波長領域 (pm~µm) において、TIEをシミュレーションすることで、光の強度分布がどのようにしてフラクタルメディアと相互作用して分散・減衰するのかを示しました (図2)。また、電子顕微鏡で観測できる短波長領域においては、フラクタル次元と強度分散 (または透過率) の非直感的なトレードオフが発生することが明らかになりました。
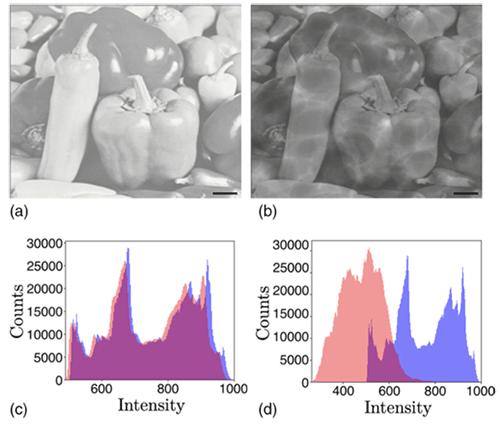
標準画像”Pepper”からなる平面波 (波長 507 nm) が、TIEに従って細胞内の光学フラクタルメディア (約10μm) を伝播するプロセスをシミュレーションした結果。(a)次元が3.25のフラクタルメディアを介したときの強度分布。スケールバーは1.00 μmを表す。(b) フラクタル次元が4.00の媒質を介したときの強度分布。(c) フラクタル次元が3.25のときの初期強度分布 (青) と最終強度分布 (赤) のヒストグラム比較。(d) フラクタル次元が4.00のときの強度ヒストグラムの比較。
(3) 細胞内の光学パラメータの計測
TIEにおける位相分布と屈折率ゆらぎを数学的に結ぶ関数を導出することに成功し、蛍光イメージングから細胞内部の屈折率ゆらぎ・フラクタル次元・散乱係数などの光学的特性を再構築できるようになりました。
今後の研究の展望
本研究成果は、細胞内の光学特性の不均一な空間分布によって引き起こされる光散乱とゆらぎを細胞モデルに組み込むことで、「生物画像シミュレーション」の拡張実装が可能になります。このようなシミュレーションの改良は、特に、データサイエンスで暗黙的に仮定されている観測的不変性 (または対称性) の数値的評価と検証に関連しています。
用語解説
- *1 強度輸送方程式 (TIE)
- TIEは、物理学において特に光学や放射輸送理論で重要な役割を果たしており、特定の方向 (z軸) に流れる光の強度 (または一般的には何かしらの粒子や波の流量) がどのように変化するかを表している。オリジナルの強度輸送方程式は光の強度が任意の位相分布を進むときに、その強度がどのように伝搬するかを記述する。つまり、光や電子の波が位相分布を通過する際のその振る舞いを理解するための基本的な数学的表現となっている。具体的には、光が物質を透過する際の強度の変化を数学的に表現し、計算することが可能になる。また、これは放射線治療や医用画像化、大気光学、天体物理学など、多くの科学技術分野において重要な役割を果たしている。
- *2 光学フラクタルモデル (またはメディア)
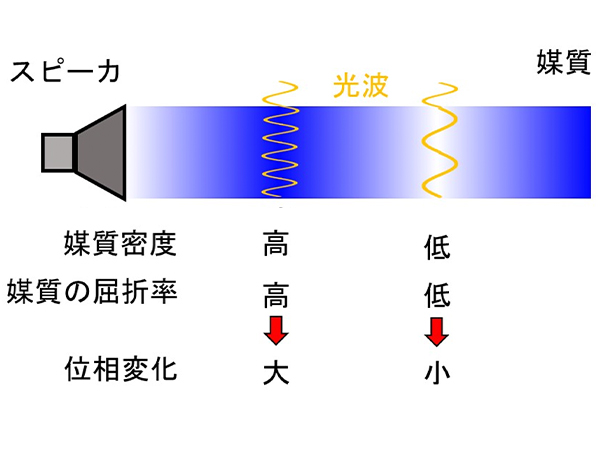
- 細胞内の屈折率分布は、空間的フラクタルの特性を兼ね備えており、分布全体と部分が自己相似の関係にある。2010年ごろに米国ノースウェスタン大学のV.ブラックマンの研究チームが、特に、Whittle-Matern共分散と呼ばれる相関関数を用いて、屈折率の空間的揺らぎにおけるランダムフィールドのモデリングを行った。
- *3 蛍光イメージング
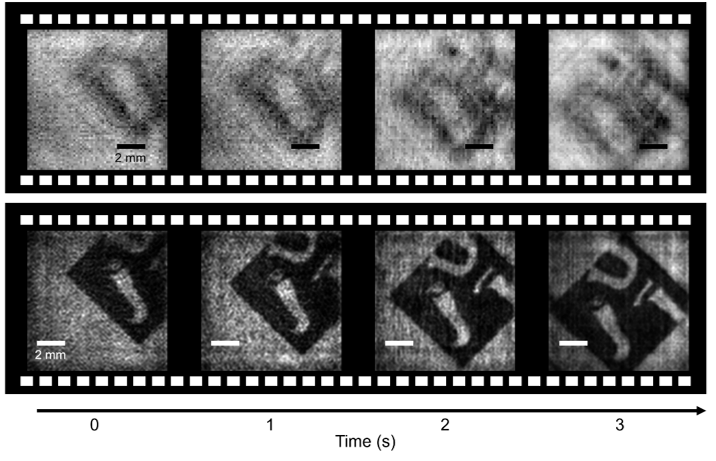
- 特定の分子や構造を視覚化するための強力な技術。特定の物質に蛍光物質を結合させ、特殊な光源 (通常はレーザー) を当てることでその物質を「光らせる」ことによって機能する。蛍光物質は、特定の波長の光を吸収し、それを別の波長 (通常はより長い) で放出する。この特性により、観察者は背景のノイズから蛍光シグナルを区別することができる。蛍光イメージングは生物学的な研究で広く用いられており、例えば、特定のタンパク質の位置や活動の追跡や、生物の組織や細胞内での化学反応の観察に用いられる。
研究サポート
本研究は、科研費学術変革領域 (A) (20H05886, 領域代表; 的場修, 20H05891, 計画研究分担; 平野泰弘, 21H05605, 公募研究代表; 渡部匡己)、及び、科研費挑戦的萌芽 (20K21836、研究代表; 渡部匡己)の支援を受けて実施されました。
論文情報
- タイトル
- “Optical dispersions through intracellular inhomogeneities”
- DOI
- 10.1103/PhysRevResearch.5.L022043
- 著者
- 渡部匡己*, 平野泰弘, 岩根敦子, 的場修, 高橋恒一
- 掲載誌
- Physical Review Research