Researchers at Kobe University and Osaka University have successfully developed artificial intelligence technology that can extract hidden equations of motion from regular observational data and create a model that is faithful to the laws of physics.
This technology could enable us to discover the hidden equations of motion behind phenomena for which the laws were considered unexplainable. For example, it may be possible to use physics-based knowledge and simulations to examine ecosystem sustainability.
The research group consisted of Associate Professor YAGUCHI Takaharu and PhD. student CHEN Yuhan (Graduate School of System Informatics, Kobe University), and Associate Professor MATSUBARA Takashi (Graduate School of Engineering Science, Osaka University).
These research achievements were made public on December 6, 2021, and were presented at the Thirty-fifth Conference on Neural Information Processing Systems (NeurIPS2021), a prestigious meeting on artificial intelligence technologies. This research was among the top 3% selected for the spotlight category.
Main points
- Being able to model (formularize) physical phenomena using artificial intelligence could result in extremely precise, high-speed simulations.
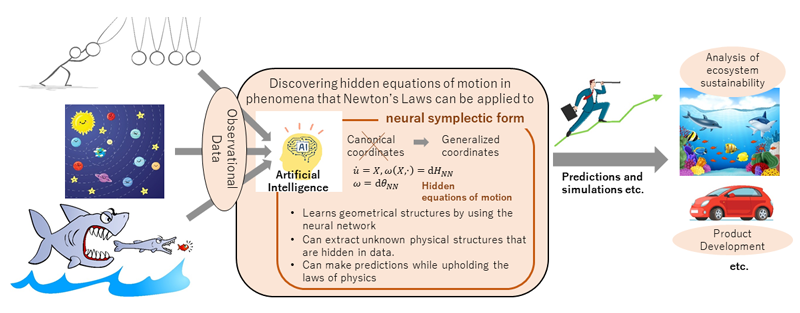
- In current methods using artificial intelligence, it is necessary to use transformed data that fits the equation of motion. Therefore it is difficult to apply artificial intelligence to actual observational data for which the equations of motion are unknown.
- The research group used geometry to develop artificial intelligence that can find the hidden equation of motion in the supplied observational data (regardless of its format) and model it accordingly.
- In the future, it may be possible to discover the hidden physical laws behind phenomena that that had previously been considered to be incompatible with Newton’s Laws, such as ecosystem changes.
- This will enable us to carry out investigations and simulations related to these phenomena using the laws of physics, which could reveal previously unknown properties.
Research Background
Ordinarily, predictions of physical phenomena are carried out via simulations using supercomputers. These simulations use mathematical models based on the laws of physics, however if the model is not highly reliable then the results will also lack reliability. Therefore, it is essential to develop a method of producing highly reliable models from the observational data of phenomena. Furthermore, in recent years the range of physics applications has expanded beyond our predications, and it has been demonstrated that it is possible to apply Newton’s Laws to other aspects, such as part of a model to show ecosystem changes. However, a concrete equation of motion has not yet been revealed for many cases.
Research Methodology
This research study developed a method of discovering novel equations of motion in observational data for phenomena that Newton’s Laws can be applied to. Previously, research has been conducted into discovering equations of motion from data, however the prior method required the data to be in the appropriate format to fit its assumed special form of the equation of motion. However, there are many cases in reality where it is not clear what data format is best to use, therefore it is difficult to apply realistic data.
In response to this, the researchers considered that the appropriate transformation of observational data is akin to coordinate transformation in geometry, thus resolving the issue by applying the geometric idea of coordinate transformation invariance found in physics. For this, it is necessary to illuminate the unknown geometric properties behind phenomena. The research team subsequently succeeded in developing AI that can find these geometric properties in data. If equations of motion can be extracted from data, then it will be possible to use these equations to create models and simulations that are faithful to physical laws.
Further Developments
Physics simulations are carried out in a wide range of fields, including weather forecasting, drug discovery, building analyses, and car design, but they usually require extensive calculations. However, if AI can learn from the data of specific phenomena and construct small-scale models using the proposed method, then this will simplify and speed up calculations that are faithful to the laws of physics. This will contribute towards the development of the aforementioned fields. Furthermore, we can apply this method to aspects that at first glance appear to be unrelated to physics. If equations of motion can be extracted in such cases, this will make it possible to do physics knowledge-based investigations and simulations even for phenomena that has been considered impossible to explain using physics. For example, it may be possible to find a hidden equation of motion in animal population data that shows the change in the number of individuals. This could be used to investigate ecosystem sustainability by applying the appropriate physical laws (eg. the law of conservation of energy, etc.).
Acknowledgements
This research received funding from the following:
- The Japan Science and Technology Agency (JST)’s CREST (Core Research for Evolutional Science and Technology) funding program for team research:
Research Area: “Creating information utilization platform by integrating mathematical and information sciences, and development to society” (Research Supervisor: UEDA Naonori).
Research Project Title: “Structure Preserving System Modeling and Simulation Basis Based on Geometric Discrete Mechanics” (Grant Number JPMJCR1914) (Research Director: Yaguchi Takaharu).
Journal Information
- Title
- “Neural Symplectic Form: Learning Hamiltonian Equations on General Coordinate Systems”
- Authors
- Yuhan Chen1, Takashi Matsubara2, Takaharu Yaguchi1
- Graduate School of System Informatics, Kobe University
- Graduate School of Engineering Science, Osaka University
- Journal
- Advances in Neural Information Processing Systems 34 (NeurIPS 2021)










